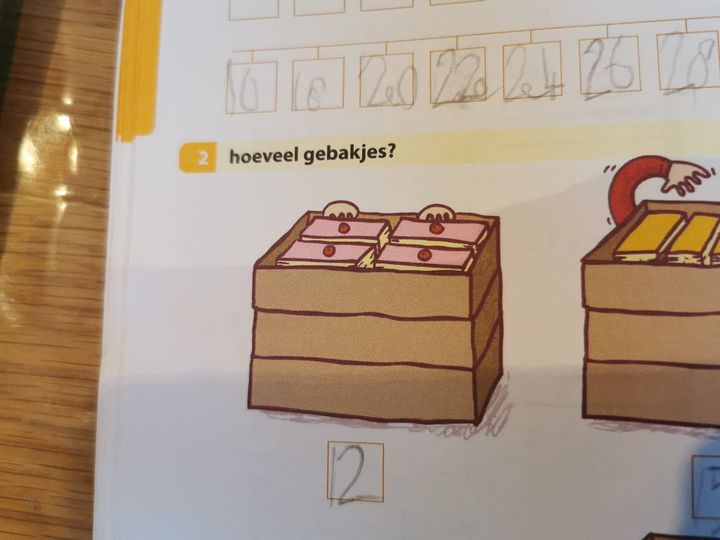
Omdat er tijdens de lockdown veel thuisonderwijs werd gegeven, keken ouders ook vaker over de schouders van hun kind mee, wat er op school wordt onderwezen. Zo verscheen er op de Facebookpagina van Pharos (oudervereniging van hoogbegaafde kinderen) een foto van een rekentaak van een kind uit groep 3. Te zien zijn drie dozen met vier gebakjes erin. Kind had keurig in het antwoordvakje “12” geschreven.
De juf had vervolgens in haar online-les gevraagd: “Welke keersom hoort hierbij?” Zoon had geantwoord: “4×3”. Juf: “Nee, de uitkomst is hetzelfde, maar het is echt anders!” De moeder had om opheldering gevraagd bij de juf en de juf had aangegeven, dat het met een tekening erbij echt anders is.
Op dit bericht kwamen meer dan 100 reacties. Ik heb zelf ook gereageerd en dacht ervan af te zijn met de eenvoudige opmerking dat voor vermenigvuldigen een commutatieve eigenschap geldt. Dat bleek van mij een verkeerde inschatting. Gaandeweg ontstonden er twee kampen: een kamp van mensen (voornamelijk bevolkt door juffen) die vonden dat 3×4 het enig juiste antwoord was, en een kamp van mensen (ouders, waaronder wiskundigen, ingenieurs en/of academisch opgeleiden), die ook het antwoord 4×3 goedgekeurd wilden zien.
Tot mijn verbazing kwamen de twee kampen geen millimeter dichter tot elkaar. En ik ben enkele juffen dankbaar, dat zij bereid waren hun visie breed uiteen te zetten (en vasthoudend te verdedigen). Zij betoogden dat het hier “om context en syntaxis gaat”. De context is het plaatje en “het is de bedoeling om bij de gegeven afbeelding te blijven.” Het belang van syntaxis werd als volgt uitgelegd. In dat plaatje zie je “3 dozen met elk 4 gebakjes, dus 3×4. Als je denkt: ik zie 4 gebakjes en dat 3x, dan lijkt het of je 4×3 zegt, maar je zegt: 4 en dat dan 3x.” Hoewel er juffen bij waren, die verkondigden dat “op abstract (of formeel) niveau 3×4 gelijk is aan 4×3”, hielden ze vol, dat hier “ook al is de uitkomst wel gelijk, de som van 3×4 niet dezelfde is als de som 4×3.” Alsof het toeval is, dat die uitkomst hetzelfde is!
Er was een juf bij, die zich echt uitputte om ons, ouders, op het rechte spoor te krijgen. Ik had iets geroepen over bottom-up benadering. Zij schrijft: “Dit heeft niets te maken met top-down of bottom-up, maar alles met inzicht in wat een vermenigvuldiging eigenlijk is en uit welke componenten een geschreven vermenigvuldiging bestaat. (…) De fout die hier door meerdere mensen wordt gemaakt, is de onterechte aanname, dat ‘4 en dat 3x’ 4x 3 is. Terwijl ‘4 en dat 3x’ niets anders is dan ‘3x 4’. (…) Een kind dat dit niet ziet, is niet extra hb, extra ver, of extra creatief, maar mist inzicht. En daar zijn leerkrachten voor, om hen dat te leren.”
Daar had ze een raak punt: inzicht in vermenigvuldiging geven vind ik zelf ook heel belangrijk. Ze schreef: “‘vermenigvuldigen met’ is herhaald optellen. Je telt dus op: 4+4+4 (dat is 3×4). Dat klopt ook bij deze tekening. Ik kan dat zien.” Maar wat ze bewust niet wílde zien, is dat je ook op een andere manier kan kijken. Dus ik maakte voor haar een tekening met een nieuwe doos en dit keer was de bakker jarig. Hij had in zijn dozen feestgebakjes gestopt in vier kleuren. Ik had de doos doorzichtig gelaten, zodat je duidelijk stapeltjes roze, oranje, groene gebakjes kon zien en dat blauwe stapeltje kon je er wel bij voorstellen, leek me.

Kortom: 4+4+4 (3×4) of 3+3+3+3 (4×3), het maakt allemaal helemaal niets uit. Zelfde context, alleen even iets verder kijken dan jouw eigen methode. Maar daar kon deze juf niets mee: “Sorry voor jou, maar bij het gegeven plaatje past maar één correcte keersom. Take it or leave it.” Een ander reageert met: “dat is erg ingewikkeld en geen juiste strategie voor de toekomst. Zeker niet als de groepjes groter worden.” Nog weer een ander zegt: “Ik ben leerkracht en in de opleiding hebben we geleerd dat het echt wel 3×4 is in dit geval…”
Meerdere juffen betoogden dat het nu eenmaal ging “om het principe erachter dat ze in groep 3 leren. (…) Dan zijn de groep 3 regels zo (los van of dat wiskundig dus anders wordt gezien) dat je begint met 3x het groepje van 4.” En omdat juffen juffen zijn, zat er ook iets heel goeds achter: “Voor kinderen waarbij het rekenbegrip zwakker is, is het belangrijk om het ook talig te maken. Daarom maken ze er een zinnetje/verhaaltje van om hen te ondersteunen: je ziet 3 KEER 4 gebakjes. Andersom lukt dat niet goed. Je ziet vier keer drie… is een zinnetje dat dan even niet klopt.” Deze laatste juf vond het dan nog wel een beetje onrechtvaardig voor de sterke rekenaars. En gelukkig reageerden er ook enkele leerkrachten, die zeiden beide antwoorden goed te keuren.
Eerlijk gezegd: ik was met stomheid geslagen. Volgens mij verwarren ze middel met doel. Je kunt zo’n plaatje met gebakjes heel goed als middel gebruiken om uit te leggen wat vermenigvuldigen is. En ik snap dat je voor de zwakkere rekenaar eenduidige taal gebruikt en daarom eerst het aantal groepjes noemt en daarna de hoeveelheid binnen zo’n groepje.
Maar nergens in de wiskunde of rekenkunde heerst een regel, die dit als enige mogelijkheid bestempelt. Dit is echt iets dat door goedbedoelende pedagogen en/of methodeschrijvers is verzonnen. En dat blijkbaar als harde eis op de Pabo terecht is gekomen…en in het antwoordmodel van online rekenprogramma’s voor groep 3.
Als over die regel door een ouder een vraag wordt gesteld, antwoordt een juf: “dat kan je onzin vinden, maar dat is het niet. Het gaat om volgordelijk denken. Als je kijkt naar het drieslagmodel gaat het om het plannen van de som. Vanuit context ( in dit geval de afbeelding) naar bewerking. Zonder context, dus een kale som, heb je gelijk en is 3×4 eenzelfde uitkomst als 4×3. Sterker nog, de kinderen leren dit als één van de strategieën.” Alweer verwarring van middel met doel. Mij lijkt het inzicht, dat 3×4 gelijk is aan 4×3 juist een doel, en geen strategie. Alsof het louter een trucje is, dat je kan toepassen om een oplossing te krijgen van je rekensommetje.
Waar het in mijn ogen vooral misgaat, is als je als juf blijft vasthouden aan je misplaatste gelijk en iets gaat fout rekenen, wat één of twee klassen later juist goed is. Een juf zegt: “En daar is een reden voor, namelijk dat de kinderen in een hogere groep leren dat je de sommen kunt omdraaien en dezelfde uitkomst houdt. Pas dan komt het wiskundige gelijk om de hoek kijken.”
Hier komen we bij de kern van mijn ongenoegen: pas dán! Dán pas mag een kind, dat nieuwsgierig is naar rekenen en er lol in heeft, zijn inzicht verder uitbouwen. Maar ik heb kinderen in mijn plusklas, die 5 jaar oud zijn en al rekenen op het niveau van groep 6. Ik heb een kind, dat in groep 3 al alle tafels op kon zeggen. Of ik ze wel wilde horen? Natuurlijk! En hij sprong en zong vrolijk rond onze middentafel een heleboel rondjes (tien tafels opzeggen duurt best lang). Later bleek mij, dat hij in zijn eigen klas mismoedig in een hoekje zit te werken, bang dat hij zijn taakjes niet afkrijgt, omdat hij zo langzaam werkt. Hij háát school. En dit soort kinderen krijgt dan te horen dat 4×3 fout is!
Wat moet je met dit soort juffen? Ik heb er ook geen antwoord op, helaas. Ik zou willen dat ze één enkel keertje in mijn plusklas zouden komen kijken. Ik zou willen dat ze naar het kind zelf zouden kijken. Ik zou willen dat ze tegen het kind, dat 4×3 als antwoord geeft, zouden zeggen: “Okay, en weet je misschien nóg een keersom? En weet je misschien ook nog een derde en een vierde keersom, die bij dit plaatje past?” Want in hemelsnaam, waarom zou 1×12 fout zijn? En ik kan ook de linkerkant en de rechterkant van de stapel taartdozen bij elkaar optellen: 6+6 gebakjes maakt 2×6.
Dat zijn pas interessante vragen voor een hoogbegaafde.
